链表 | Hongxu's Blog

定义

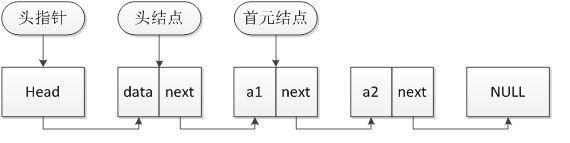
链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构，操作复杂。由于不必须按顺序存储，链表在插入的时候可以达到O(1)的复杂度，比另一种线性表顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要O(n)的时间，而线性表和顺序表相应的时间复杂度分别是O(logn)和O(1)。
使用链表结构可以克服数组链表需要预先知道数据大小的缺点，链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理。但是链表失去了数组随机读取的优点，同时链表由于增加了结点的指针域，空间开销比较大。链表最明显的好处就是，常规数组排列关联项目的方式可能不同于这些数据项目在记忆体或磁盘上顺序，数据的存取往往要在不同的排列顺序中转换。链表允许插入和移除表上任意位置上的节点，但是不允许随机存取。链表有很多种不同的类型：单向链表，双向链表以及循环链表。

定义

LeetCode 练习题

两数相加 LeetCode#2

给出两个 非空 的链表用来表示两个非负的整数。其中，它们各自的位数是按照 逆序 的方式存储的，并且它们的每个节点只能存储 一位 数字。
如果，我们将这两个数相加起来，则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外，这两个数都不会以 0 开头。
示例：

输入：(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出：7 -> 0 -> 8
原因：342 + 465 = 807

1. 先求解再转为链表

• 遍历两链表求出两数
• 两数相加求和
• 数字再转为链表

这是相对来说比较直观的一种解法，关键就在链表转数字以及数字转链表

空间复杂度和时间复杂度都不是很理想

const ListNode = (val) => {
  this.val = val
  this.next = null
}

const number2List = (num) => {
  const numArr = String(num).split('').map(item => Number(item))
  const head = new ListNode()
  let curNode = head
  const len = numArr.length
  for (let i = len; i > 0; i--) {
    curNode.val = numArr[i - 1]
    curNode.next = i === 1 ? null : new ListNode()
    curNode = curNode.next
  }
  return head
}

const list2Number = (list) => {
  let weight = 0
  let num = 0
  while(list !== null) {
    const curNum = list.val * Math.pow(10, weight)
    num += curNum
    weight += 1
    list = list.next 
  }
  return num
}

const addTwoNumbers = (l1, l2) => {
  if (l1 === null) {
    return l2
  }

  if (l2 === null) {
    return l1
  }
  const number1 = list2Number(l1)
  const number2 = list2Number(l2)
  const sum = number1 + number2
  return number2List(sum)
}

但是出错啦 TAT

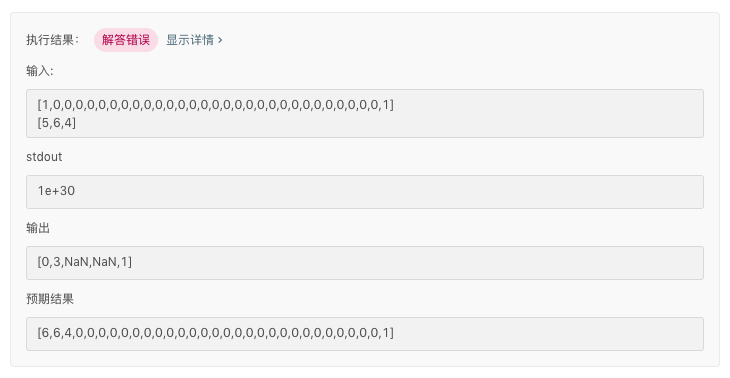
这就是没有考虑到超大数字。
不仅如此，如果最后的结果是 Infinity 这个方法就不起作用了。

2. 遍历两链表，用变量表示是否进位

• 两链表对应位置值相加
• 标志位有进位设为 1 无进位就设为 0（仅限两链表相加）

时间复杂度是 O(n) 空间复杂度是 O(n)

这里需要注意几种情况

1. 链表位数不相同
2. 最终结果值大于两链表最大位数

const addTwoNumbers = (l1, l2) => {
  if (l1 === null) {
      return l2
  }
  if (l2 === null) {
      return l1
  }
  const head = new ListNode(0)
  let list1 = l1
  let list2 = l2
  let curNode = head
  let carry = 0

  while (list1 !== null || list2 !== null) {
    const num1 = list1 === null ? 0 : list1.val
    const num2 = list2 === null ? 0 : list2.val
    // 这里注意不要忘记加进位的数
    const sum = num1 + num2 + carry
    // 处理进位
    carry = sum >= 10 ? 1 : 0
    curNode.next = new ListNode(sum % 10)
    curNode = curNode.next
    // list 长度不一致的时候的特殊处理
    if (list1 !== null) {
      list1 = list1.next
    }

    if (list2 !== null) {
      list2 = list2.next
    }
  }
  // 遍历完后还有数字的特殊处理
  if (carry !== 0) {
    curNode.next = new ListNode(carry)
  }
  // 这里注意要返回 head 的 next 应为刚开始我们构造了一个无效的 Node 来辅助我们解题
  return head.next
}

删除链表的倒数第N个节点 LeetCode#19

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。
示例：

给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后，链表变为 1->2->3->5.

说明：
给定的 n 保证是有效的。
进阶：
你能尝试使用一趟扫描实现吗？

总之就是有一个 ListNode
需要将 LN(n - 1) 的 next 指针 指向 LN(n + 1) 即
LN(n - 1).next = LN(n + 1) 即
LN(n - 1).next = LN(n - 1).next.next

1. 数组存放链表信息

我首先想到的是这么解

• 遍历一遍链表并挨个放到数组里面
• 对应修改 n - 1 的 next 节点到 n + 1

这里要注意

1. n - 1 和 n + 1 是否存在

这么解时间复杂度是 O(n) 但是由于引入一个数组所以是 O(n) 的空间复杂度

const removeNthFromEnd = (head, n) => {
  if (head === null) {
    return head
  }
  // 遍历一遍并存放链表数据
  const memory = []
  while (head !== null) {
    memory.push(head)
    head = head.next
  }
  // 当只有一个节点的特殊处理
  const len = memory.length
  if (len === 1) {
    return memory[0].next
  }

  const index = len - n
  // 当 n = 0 的特殊情况，此时不删除任何节点（因为题目说保证 n 有效，所以先注释掉）
  // if (index === len) {
  //   return memory[0]
  // }
  // 当 n = 链表总长度的特殊情况，此时无 n - 1
  if (index === 0) {
    return memory[1]
  }

  // 注意这里的 memory[index + 1] || null 是为了处理 n + 1 不存在的情况
  memory[index - 1].next = memory[index + 1] || null
  return memory[0]
}

但是有没有更好的解法

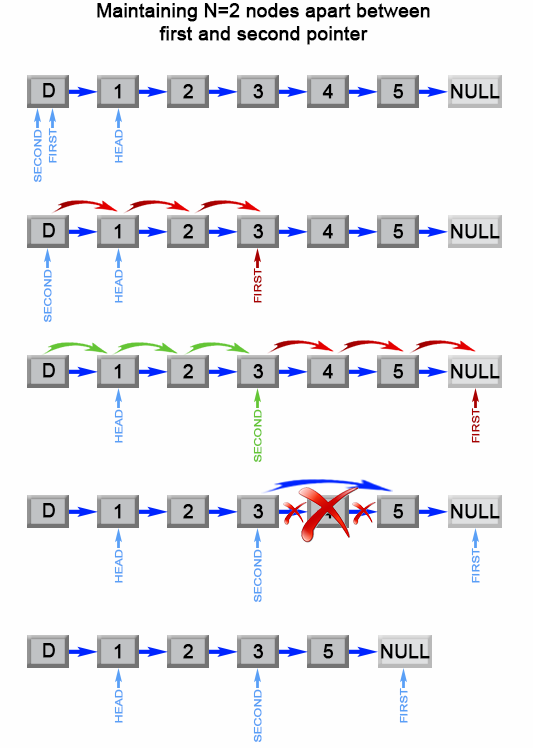
2. 双指针法

这是 LeetCode 中文官方的一个解
思路就是有两个指针，第一个在前是 forwardP 另一个滞后与他 n + 1 个 Node
这样当第一个指针跑到最后时，第二个指针刚好就在倒数第 n - 1 个位置

这样就优化了之前存放临时数据的数组的空间

时间复杂度是 O(n) 空间复杂度是 O(1)

• 两个指针初始位置都在头节点
• 指针 1 先向前走 n 个节点
• 两指针同时前进，当指针 1 跑到链表尾时更改指针 2 指向

const removeNthFromEnd = (head, n) => {
  // 引入一个 head node 可以避免下面的很多判断
  const _head = new ListNode()
  _head.next = head

  let forwardPointer = _head;
  let pointer = _head;

  // 指针 1 前进 n + 1步
  for (let step = 1; step <= n + 1; step++) {
    forwardPointer = forwardPointer.next
  }
  // 双指针同时前进
  while (forwardPointer !== null) {
    forwardPointer = forwardPointer.next
    pointer = pointer.next
  }
  // 删除第 n 个位置的值
  pointer.next = pointer.next.next
  return _head.next
}

合并两个有序链表 LeetCode#21

将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例：

输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

1. 遍历两链表

首先想到的是如下思路
思路：增加一个主链表，依次比较两链表的将小的节点加入主链表，最后将主链表返回

时间复杂度是 O(m + n) 空间复杂度是 O(1)

• 比较两链表的当前节点
• 将值小的节点加入主链表
• 当有一个节点遍历到最后时将另一个链表的当前节点加入主链表

const mergeTwoLists = (l1, l2) => {
  // l1 l2 为空的特殊处理
  if (l1 === null) {
      return l2
  }
  if (l2 === null) {
      return l1
  }

  const _head = new ListNode();
  let pointer = _head
  // 注意这里的遍历条件当有一个已经遍历完了之后就停止
  while (l1 !== null && l2 !== null) {
    const l1IsMin = l1.val < l2.val
    pointer.next = l1IsMin ? l1 : l2
    if (l1IsMin) {
      l1 = l1.next
    } else {
      l2 = l2.next
    }
    pointer = pointer.next
  }

  pointer.next = l1 === null ? l2 : l1
  return _head.next
}

2. 递归法 - LeetCode 解法1

递归法只需要关注边界条件已经处理单节点逻辑，这样的话代码结构会比较清晰

注意终止条件是 node === null

时间复杂度是 O(m + n) 空间复杂度是 O(m + n)

const mergeTwoLists = (l1, l2) => {
  // l1 l2 为空的特殊处理
  if (l1 === null) {
      return l2
  }
  if (l2 === null) {
      return l1
  }
  // 选择值小的节点返回并处理 next 指向为递归结果
  if (l1.val < l2.val) {
    l1.next = mergeTwoLists(l1.next, l2)
    return l1
  }

  l2.next = mergeTwoLists(l1, l2.next)
  return l2
}

合并K个排序链表 LeetCode#23

这题是 合并两个有序链表的变种，我首先想到的方法与 #21-1 是同样的解法，只不过由比较两个数的大小改为比较 K 个数的大小。

1. 遍历 K 个链表

这种解法的时间复杂度是 O(k * n)，空间复杂度是 O(n)

const findMinIndex = (lists) => {
  const len = lists.length
  let min = null
  let minIndex = -1
  for (let i = 0; i < len; i++) {
    if (lists[i] === null) {
      continue
    }
    if (min === null) {
      min = lists[i].val
      minIndex = i
      continue
    }
    const curVal = lists[i].val
    if (curVal < min) {
      minIndex = i
      min = curVal
    }
  }
  return minIndex
}

var mergeKLists = function(lists) {
  let listLen = lists.length
  // 处理特殊情况
  if (listLen === 0) {
    return null
  }
  const head = new ListNode()
  let pointer = head

  while (listLen > 0) {
    minIndex = findMinIndex(lists)
    if (minIndex < 0) {
      return head.next
    }
    pointer.next = lists[minIndex]
    pointer = pointer.next
    lists[minIndex] = lists[minIndex].next
  }
  return head.next
}

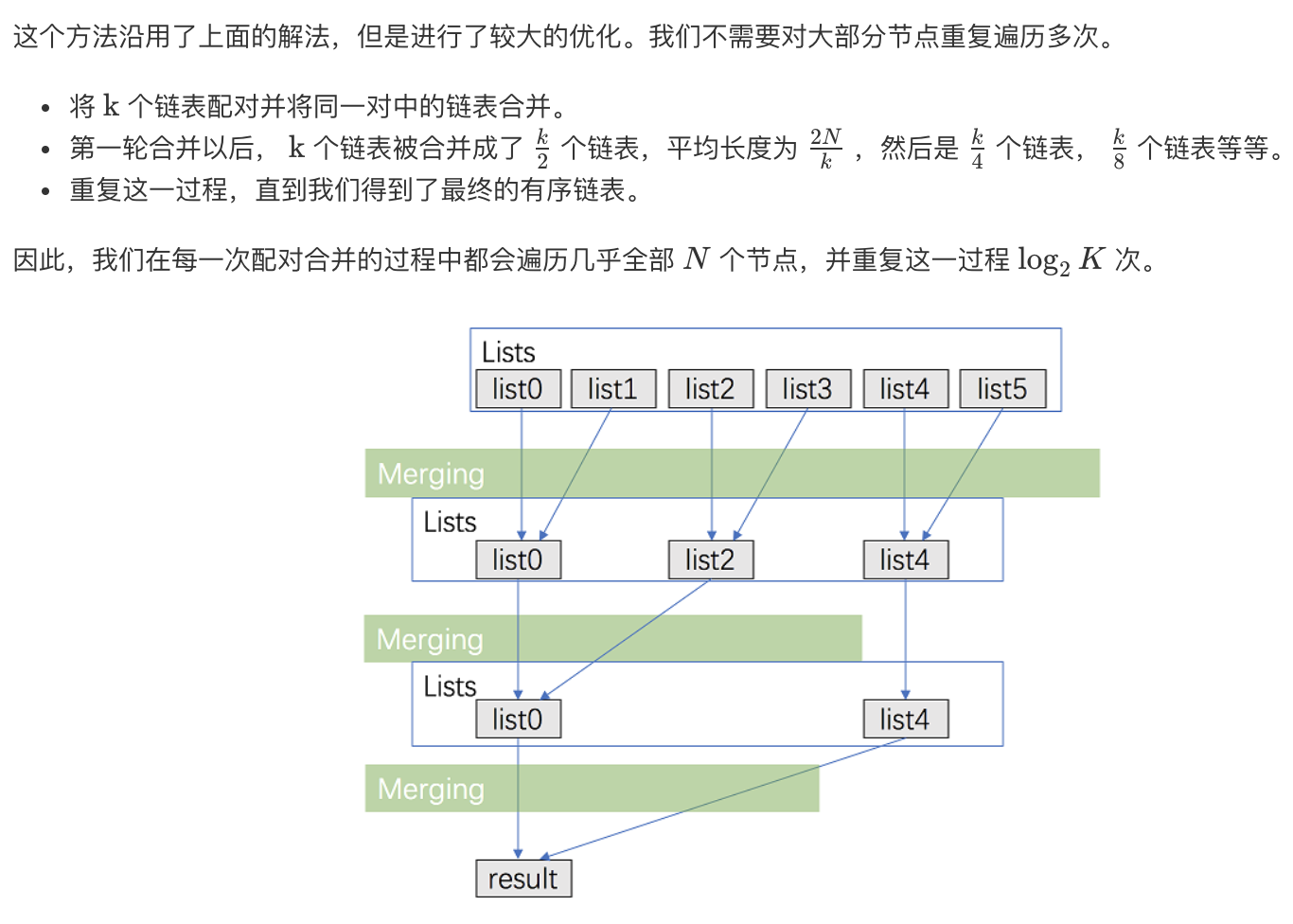
2. 分治思想

这是 LeetCode 官方解答之一

const mergeKLists = (lists) => {
  const len =  lists.length
    let interval = 1
    while (interval < len) {
      for(let i = 0; i < len - interval; i = i + interval * 2) {
        lists[i] = mergeTwoLists(lists[i], lists[i + interval])
      }
      interval = interval * 2
    }
    return len > 0 ? lists[0] : null
}

两两交换链表中的节点 LeetCode#24

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。
你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。
示例:

给定 1->2->3->4, 你应该返回 2->1->4->3.

1. 遍历

每次循环的 step 相当于等于 2
注意终止条件有两个一个是当前节点为 null 另一个是 next 节点为 null

该方法时间复杂度是 O(n)，由于创建新的链表顾空间复杂度也为 O(n)

const swapPairs = (head) => {
  if (head === null) {
    return head
  }
  const _head = new ListNode()
  // 指向返回链表的当前节点
  let cursor = _head
  // 指向原始链表的当前节点
  let pointer = head
  while (pointer !== null) {
    if (pointer.next === null) {
      cursor.next = new ListNode(pointer.val)
      cursor = cursor.next
      break
    }
    // 交换链表节点值
    cursor.next = new ListNode(pointer.next.val)
    cursor.next.next = new ListNode(pointer.val)
    // 循环步长为 2
    cursor = cursor.next.next
    pointer = pointer.next.next
  }
  // 注意处理尾节点的 next 为 null
  cursor.next = null
  return _head.next
}

2. 递归法

const swapPairs = (head) => {
  // 特殊处理
  if (head === null || head.next === null) {
    return head
  }
  const next = head.next
  head.next = swapPairs(next.next)
  next.next = head
  return next
}

K 个一组翻转链表 LeetCode#25

给你一个链表，每 k 个节点一组进行翻转，请你返回翻转后的链表。
k 是一个正整数，它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。
示例:

给定这个链表：1->2->3->4->5
当 k = 2 时，应当返回: 2->1->4->3->5
当 k = 3 时，应当返回: 3->2->1->4->5

说明:
你的算法只能使用常数的额外空间。
你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

这题我的想法是两个指针 一个指向每次要翻转的最后一个节点记为 lastNode，另一个指针从当前要反转的起始位置开始一直走到最后一个节点 记为 curNode，每次走的时候 lastNode -> curNode，来实现翻转的目的。
但是提交的时候各种边界条件没有考虑清楚，提交了很多次都没 ac。

1. 遍历

好吧这题太难了，下次再做 😝
国际惯例记一个 TODO

旋转链表 LeetCode#61

给定一个链表，旋转链表，将链表每个节点向右移动 k 个位置，其中 k 是非负数。
示例 1:

输入: 1->2->3->4->5->NULL, k = 2
输出: 4->5->1->2->3->NULL
解释:
向右旋转 1 步: 5->1->2->3->4->NULL
向右旋转 2 步: 4->5->1->2->3->NULL

示例 2:

输入: 0->1->2->NULL, k = 4
输出: 2->0->1->NULL
解释:
向右旋转 1 步: 2->0->1->NULL
向右旋转 2 步: 1->2->0->NULL
向右旋转 3 步: 0->1->2->NULL
向右旋转 4 步: 2->0->1->NULL

1. 暴力解法

这是我最先想到的解法，把node 信息放到一个数组里
更具 k 依次遍历对应 Node 进行旋转

时间复杂度 O(n + k) 空间复杂度 O(n)

// 根据右旋值 i 计算应当移动的节点在数组的哪个位置
const calcIndex = (len, i) => {
  if(len > i) {
    return len - i
  }
  const rest = i % len
  let index = 0
  if (rest) {
    index = len - rest
  }
  return index
}

const rotateRight = (head, k) => {
  // 特殊情况
  if (k === 0) {
    return head
  }
  const allLinks = []
  let pointer = head
  // 获取链表的所有信息
  while (pointer !== null) {
    allLinks.push(pointer)
    pointer = pointer.next
  }
  const linksLen = allLinks.length
  // 无链表数据及只有 1 个链表数据
  if (linksLen === 0 || linksLen === 1) {
    return head
  }
  // 无效右旋过滤
  k = k % linksLen
  let _head = head
  // 开始右旋
  for (let i = 1; i <= k; i++) {
    const index = calcIndex(linksLen, i)
    const prevNodexIndex = calcIndex(linksLen, i + 1)
    const curNode = allLinks[index]
    const prevNode = allLinks[prevNodexIndex]
    curNode.next = _head
    prevNode.next = null
    _head = curNode
  }
  return _head
}

2. 形成环链表法

这种解法也是 LeetCode 官方解法之一。
其思路就是将链表构成一个环，再在对应的地方切断。就自然而然的形成了右移

时间复杂度 O(2n - k) 空间复杂度 O(1)

const rotateRight = (head, k) => {
  // 特殊情况处理
  if(head === null || head.next === null || k === 0) {
    return head
  }

  // 留住头结点翻遍成环
  const _head = head
  let linkLen = 1;
  // 先找到尾节点，并得出链表长度用于后续计算 拆开节点位置
  while (head.next !== null) {
    head = head.next
    linkLen += 1
  }

  // 形成闭环
  head.next = _head
  // 计算在何处拆开节点
  // 这一步决定了结果是否正确非常重要
  // 这里计算要移动的位置是返回值的表尾，表尾 next 就是返回值的 表头
  const breakKey = linkLen < k ? linkLen - (k % linkLen) : linkLen - k
  // 移动到该节点
  for (let i = 1; i <= breakKey; i++) {
    head = head.next
  }
  // 拆开环链表
  const rHead = head.next
  head.next = null
  return rHead
}

删除排序链表中的重复元素 II LeetCode#82

给定一个排序链表，删除所有含有重复数字的节点，只保留原始链表中 没有重复出现 的数字。
示例 1:

输入: 1->2->3->3->4->4->5
输出: 1->2->5

示例 2:

输入: 1->1->1->2->3
输出: 2->3

因为是有序链表，所以依次遍历，比较当前节点与上一个节点和下一个节点是否一致如果有重复就不返回

时间复杂度 O(n) 空间复杂度 O(1)

const deleteDuplicates = (head) => {
  const result = new ListNode()
  let point = result

  let cur = head
  let prev = new ListNode(null)

  while (cur !== null) {
    /* 两种情况可认为该节点有效
      1. 前继节点值和当前节点值不一样 且 后继几点为 null
      2. 前继节点值和当前节点值不一样 且 当前节点值和后继节点值不一样 */
    if (( prev.val !== cur.val && cur.next === null)
      || (prev.val !== cur.val && cur.val !== cur.next.val)
    ) {
      // 将当前节点加入
      point.next = cur
      point = point.next
    }

    prev = cur
    cur = cur.next
  }
  // ！！注意这里要 尾节点 next 置为 null
  point.next = null
  return result.next
}

删除排序链表中的重复元素 LeetCode#83

给定一个排序链表，删除所有重复的元素，使得每个元素只出现一次。
示例 1:

输入: 1->1->2
输出: 1->2

示例 2:

输入: 1->1->2->3->3
输出: 1->2->3

这题和 #82 很像思路也差不多
因为是有序的，直接比较当前值和下一个值是否一样
如果一样就把当前节点 next 转为其孙子节点 这样就实现了删除重复节点

时间复杂度 O(n) 空间复杂度 O(1)

const deleteDuplicates = (head) => {
  let _head = head

  while(_head) {
    // 下一个节点和当前节点重复
    if(_head.next && _head.val === _head.next.val) {
      // 删除下一个重复节点
      _head.next = _head.next.next
      // 不移动 _head 指针，下一个值继续与当前循环 _head 比较
      continue
    }
    _head = _head.next
  }
  return head
}

分隔链表 LeetCode#86

给定一个链表和一个特定值 x，对链表进行分隔，使得所有小于 x 的节点都在大于或等于 x 的节点之前。
你应当保留两个分区中每个节点的初始相对位置。
示例:

输入: head = 1->4->3->2->5->2, x = 3
输出: 1->2->2->4->3->5

思路：
两个指针一个叫 prev 一个叫 next，遍历链表的同时分别将值对应到 prev 和 next 里面
最终结束的时候再讲 prev 和 next 拼接起来并返回

时间复杂度 O(n) 空间复杂度 O(1)

const partition = (head, x) => {
  // 特殊处理
  if (head === null || head.next === null) {
    return head
  }
  // 建两个指针 prev 放 < x 的节点
  let prev = new ListNode()
  const prevHead = prev
  // next 放 >= x 的 节点
  let next = new ListNode()
  const nextHead = next
  // 遍历节点
  while (head !== null) {
    // 判断并放入节点到对应链表
    if (head.val < x) {
      prev.next = head
      prev = prev.next
    } else {
      next.next = head
      next = next.next
    }
    head = head.next
  }
  // ！！处理尾节点 next 值
  next.next = null
  // 合并
  prev.next = nextHead

  return prevHead
};

反转链表 II LeetCode#92

反转从位置 m 到 n 的链表。请使用一趟扫描完成反转。
说明:
1 ≤ m ≤ n ≤ 链表长度。
示例:

输入: 1->2->3->4->5->NULL, m = 2, n = 4
输出: 1->4->3->2->5->NULL

1. 拼接法

依次遍历，并记录关键节点和链表

x < m 时记录 prev
x = m 时记录 mNode
当 m < x <= n 时将当前节点插入 mNode 之前
x = n 时记录 nNode
记录 nNode.next 为 next

那最终结果就是 prev -> nNode ~ mNode -> next 且 nNode ~ mNode 已经反转好了

时间复杂度是 O(n) 空间复杂度是 O(1)

const reverseBetween = (head, m, n) => {
  if (m === n || head === null) {
    return head
  }
  const _head = new ListNode()

  let currentKey = 1

  // 第 m 个节点前面的所有节点
  let prev = _head

  // 第 m 个节点
  let mNode = null
  // 第 n 个节点
  let nNode = null
  // 第 n 个几点的后一个节点
  let next = null
  // 当前节点
  let curNode = head
  // 反向插入的几点
  let point = null

 // 最终结果 可以近似为
 // prev -> nNode -> n - m - 1 个 point 翻转而成的节点 -> mNode -> next

  while (curNode !== null) {
    const cNext = curNode.next

    // 保存 prev 链
    if (currentKey < m) {
      prev.next = curNode
      prev = prev.next
    }

    // 保存 m 节点，初始化 point 节点
    if (currentKey === m) {
      mNode = curNode
      point = mNode
    }

    // 保存 n 节点，next 节点
    if (currentKey === n) {
      nNode = curNode
      next = cNext
    }

    // 反转节点
    if(currentKey > m && currentKey <= n) {
      curNode.next = point
      point = curNode
    }

    curNode = cNext
    currentKey++
  }

  // 拼接合并节点
  prev.next = nNode
  mNode.next = next

  return _head.next
}

2. -> LeetCode 官方解答

环形链表 LeetCode#141

给定一个链表，判断链表中是否有环。
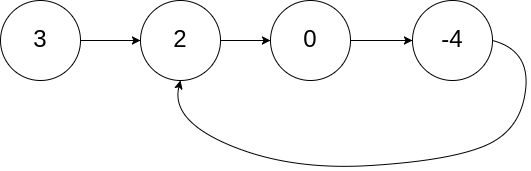
为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

示例 1：
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

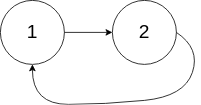
示例 2：
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：
输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

进阶：
你能用 O(1)（即，常量）内存解决此问题吗？

1. 缓存法

我的解法是用一个数组保存每个节点，然后判断 Node 是否存在于数组中，如果存在了即为有环形
但是这种算法的时间复杂度是 O(n ^ n) 空间复杂度是 O(n)

如果可以用 hash 表开存储就可以将时间复杂变为 O(n)

// arrary memory
const hasCycle = (head) => {
  if(head === null) {
    return false
  }
  const memory = []
  while (head !== null) {
    if (memory.indexOf(head) > -1) {
      return true
    }
    memory.push(head)
    head = head.next
  }
  return false
}
// hash memory
const hasCycle = (head) => {
  if(head === null) {
    return false
  }
  // set 模拟 hash table
  const memory = new Set()
  while (head !== null) {
    if (memory.has(head)) {
      return true
    }
    memory.add(head)
    head = head.next
  }
  return false
}

2. 双指针法

LeetCode 解法之二，这种解法没有想到。这里就说下 LeetCode 官方的解释。

通过使用具有 不同速度 的快、慢两个指针遍历链表，空间复杂度可以被降低至 O(1)。慢指针每次移动一步，而快指针每次移动两步。

如果列表中不存在环，最终快指针将会最先到达尾部，此时我们可以返回 false。

现在考虑一个环形链表，把慢指针和快指针想象成两个在环形赛道上跑步的运动员（分别称之为慢跑者与快跑者）。而快跑者最终一定会追上慢跑者。这是为什么呢？考虑下面这种情况（记作情况 A）- 假如快跑者只落后慢跑者一步，在下一次迭代中，它们就会分别跑了一步或两步并相遇。

const hasCycle = (head) => {
  if (head === null || head.next === null) {
    return false
  }
  let slow = head
  let fast = head.next
  while (slow !== fast) {
    // 快指针结束表示无环
    if (fast === null || fast.next === null) {
      return false
    }
    // 慢指针走一步
    slow = slow.next
    // 快指针走两步
    fast = fast.next.next
  }
  // 慢指针和快指针相遇
  return true
}