链表2
环形链表 II LeetCode#142
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
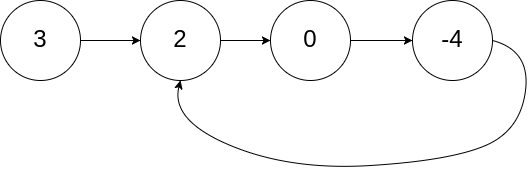
说明:不允许修改给定的链表。示例 1: 输入:head = [3,2,0,-4], pos = 1 输出:tail connects to node index 1 解释:链表中有一个环,其尾部连接到第二个节点。
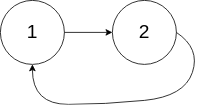
示例 2: 输入:head = [1,2], pos = 0 输出:tail connects to node index 0 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3: 输入:head = [1], pos = -1 输出:no cycle 解释:链表中没有环。
进阶:
你是否可以不用额外空间解决此题?
1. 缓存法
该解法与 LeetCode 141 的解法一样,用缓存把每个节点缓存起来,然后不断遍历链表并判断节点是否已经存在,如果已经存在就返回该节点。
这种方法的缺点也明显,时间复杂度高,空间复杂度也高
// arrary memory
const hasCycle = (head) => {
if(head === null) {
return false
}
const memory = []
while (head !== null) {
if (memory.indexOf(head) > -1) {
return true
}
memory.push(head)
head = head.next
}
return false
}
// set memory
const detectCycle = (head) => {
if(head === null) {
return head
}
// 用 set 模拟 hash table
const memory = new Set()
while (head !== null) {
if (memory.has(head)) {
return head
}
memory.add(head)
head = head.next
}
return head
}
2. Floyd 算法
该解法是在 LeetCode 141 双指针法的基础上变化而来的。如果不看答案,我是想不出这种纯数学的解法的。
分为两个阶段
- 判断是否有环
- 找出环入口(这里是一个比较巧妙的数学解法)
具体证明 -> LeetCode 142 Floyd 算法
const detectCycle = (head) => {
// 这里和 LeetCode 的双指针法有点不一样,因为这里需要严格的位置校验
let fast = head
let slow = head
let pointer = head
// 循环使快慢指针相遇
for(;;) {
if (fast === null || fast.next === null) {
return null
}
slow = slow.next
fast = fast.next.next
// 相遇时退出
if (slow === fast) {
break
}
}
// 此时 slow 多走的距离刚好是成环前的距离,所以此时用一个头指针依次和 slow 依次向后走就会在环的入口相遇
while (pointer !== slow) {
pointer = pointer.next
slow = slow.next
}
return slow
}
重排链表 LeetCode#143
给定一个单链表 L:L0→L1→…→Ln-1→Ln ,
将其重新排列后变为: L0→Ln→L1→Ln-1→L2→Ln-2→…
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。示例 1: 给定链表 1->2->3->4, 重新排列为 1->4->2->3. 示例 2: 给定链表 1->2->3->4->5, 重新排列为 1->5->2->4->3.
1. 暴力解法
思路:首先遍历一遍链表并把每个节点按顺序存放起来,第二遍按照要求从数组中取值并拼接起来链表
时间复杂度 O(n) 空间复杂度O(n)
const reorderList = (head) => {
if (head === null) {
return head
}
const memory = []
let pointer = head
// 遍历并存放节点信息
while (pointer !== null) {
memory.push(pointer)
pointer = pointer.next
}
const pRes = new ListNode()
pointer = pRes
const len = memory.length
// 按要求不断拼接 list
while(memory.length > 0) {
pointer.next = memory.shift()
pointer = pointer.next
if (memory.length > 0) {
pointer.next = memory.pop()
pointer = pointer.next
}
}
// 注意处理最后一个节点的 next 引用值,否则会溢出
pointer.next = null
return pRes.next
}
2. 反转合并法
思路:
- 用快慢指针找到链表中点
- 反转中点到链尾的链
- 合并中点前的链和中点后的链
时间复杂度 O(n) 空间复杂度O(1)
const reorderList = (head) => {
if (head === null) {
return head
}
// fast 走两步,slow 走一步,fast 走完全链时 slow 的位置就是中点
let fast = head
let slow = head
while (fast !== null && fast.next !== null) {
slow = slow.next
fast = fast.next.next
}
// 反转中点到链尾
const revertedList = revert(slow.next)
// 分割链表
slow.next = null
// 合并链表
let p1 = head
let p2 = revertedList
const pRes = new ListNode()
let pointer = pRes
while (p2 !== null) {
pointer.next = p1
pointer = pointer.next
p1 = p1.next
pointer.next = p2
pointer = pointer.next
p2 = p2.next
}
// 因为 p1 的长度总是和 p2 相等或者比 p2 大 1 个
// 所以这里要对 p1.length > p2.length 做处理
if (p1) {
pointer.next = p1
}
return pRes.next
}
const revert = (head) => {
if (head === null) {
return null
}
const pRes = new ListNode()
let pointer = head
while (pointer !== null) {
const next = pointer.next
const resNext = pRes.next
// 反转链表
// 挂载头节点
pRes.next = pointer
// 挂载当前节点
pointer.next = resNext
// 移动节点
pointer = next
}
return pRes.next
}
对链表进行插入排序 LeetCode#147
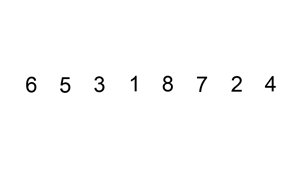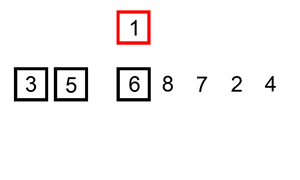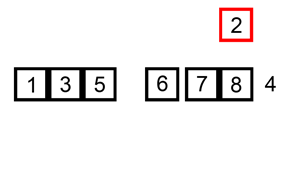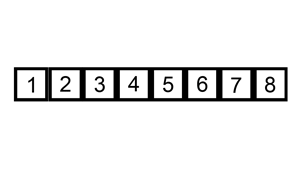
插入排序的动画演示如上。从第一个元素开始,该链表可以被认为已经部分排序(用黑色表示)。
每次迭代时,从输入数据中移除一个元素(用红色表示),并原地将其插入到已排好序的链表中。
插入排序算法:
- 插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
- 每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
- 重复直到所有输入数据插入完为止。
示例 1: 输入: 4->2->1->3 输出: 1->2->3->4示例 2: 输入: -1->5->3->4->0 输出: -1->0->3->4->5
题目已经限制了解法。如下 ↓
const insertionSortList = (head) => {
// 特殊处理
if(head === null || head.next === null) {
return head
}
// 构造辅助链表
const first = new ListNode(0)
first.next = head
// 初始化
let currentNode = head
let prevNode = null
// 遍历链表
while(currentNode !== null) {
// 不是有序数据
if (currentNode.next && currentNode.next.val < currentNode.val) {
// 找到插入位置
prevNode = first
while (currentNode.next && prevNode.next && currentNode.next.val > prevNode.next.val) {
prevNode = prevNode.next
}
// 缓存后续节点
let temp = currentNode.next
// 插入节点
currentNode.next = temp.next;
temp.next = prevNode.next;
prevNode.next = temp
} else {
// 顺序合理 或 是最后一个节点
currentNode = currentNode.next
}
}
return first.next
}